Type 1 vs type two error

Type 1 and type two errors are defined in the post-obit fashion for a null hypothesis \(H_0\):

Decision/Truth \(H_0\) true \(H_0\) false
\(H_0\) rejected Type 1 error (\(\alpha\)) Correctly rejected (Power, \(one-\beta\))
Failed to refuse \(H_0\) Correctly not rejected Blazon 2 mistake (\(\beta\))

Type 1 and type two error rates are denoted past \(\blastoff\) and \(\beta\), respectively. The power of a statistical exam is divers past \(i - \beta\). In summary:

  • The significance level answers the post-obit question: If there is no result, what is the likelihood of falsely detecting an effect? Thus, significance is a mensurate of specificity.
  • The power answers the following question: If at that place is an effect, what is the likelihood of detecting it? Thus, power is a measure of sensitivity.

The power of a examination depends on the following factors:

  • Effect size: power increases with increasing effect sizes
  • Sample size: ability increases with increasing number of samples
  • Significance level: ability increases with increasing significance levels
  • The test itself: some tests have greater ability than others for a given data set up

Traditionally, the type 1 error charge per unit is limited using a significance level of v%. Experiments are often designed for a ability of 80% using ability analysis. Note that it depends on the examination whether it's possible to determine the statistical power. For instance, ability is determined more readily bachelor for parametric than for non-parametric tests.

Choice of the null hypothesis

Since the blazon 1 error rate is typically more stringently controlled than the type 2 mistake charge per unit (i.east.\(\alpha < \beta\)), the alternative hypothesis often corresponds to the consequence you would like to demonstrate. In this style, if the zip hypothesis is rejected, it is unlikely that the rejection is a blazon 1 mistake. When statistical testing is used to inform decision making, the zilch hypothesis whose type one error would have the worse issue should exist selected. Let's consider two examples for choosing the null hypothesis in this fashion.

Example ane: introduction of a new drug

Let's assume there's a well-tried, FDA-approved drug that is constructive against cancer. Having adult a new drug, your company wants to decide whether information technology should supplant the sometime drug with the new drug. Hither, you definitely want to use a directional test in club to show that one drug is superior over the other. However, given effectivity measures A and B for the old and the new drug, respectively, how should the nothing hypothesis be formulated? Take a wait at the consequences of the choice:

Null hypothesis Type i mistake Touch on of blazon 1 fault
\(A \geq B\) Incorrectly pass up \(A \geq B\) Yous falsely conclude that drug B is superior to drug A. Thus, you introduce B to the market, thereby risking the life of patients where B was favored over A.
\(A \leq B\) Incorrectly reject \(A \leq B\) You falsely conclude that drug A is superior to drug B. Thus, albeit really superior to A, B is never released and resources take been wasted.

Evidently, having \(H_0: A \geq B\) is the more appropriate null hypothesis because its type one fault is more detrimental (lives are endangered) than that of the other nada hypothesis (patients do non receive admission to a better drug).

Example ii: modify in taxation

The government thinks about simplifying the taxation system. Permit A be the corporeality of tax income with the former, complicated system and let B exist the income with the new, simplified system.

Cypher hypothesis Type 1 error Bear upon of type i fault
\(A \geq B\) Incorrectly reject \(A \geq B\) Incorrectly conclude that the new arrangement leads to greater income. So, after changing to the simplified taxation system, y'all realize that you lot actually learn fewer taxes.
\(A \leq B\) Incorrectly reject \(A \leq B\) Incorrectly conclude that the former organization was better. You don't innovate the simplified approach and miss out on additional taxation income.

In this case, assuming that the new organization leads to less income from revenue enhancement, that is, \(H_0: A \geq B\) is clearly the ameliorate option (if you are optimizing with regard to tax income). In this instance, a type 1 error ways that the revenue enhancement system doesn't have to be changed. Using the other null hypothesis, a type i error would hateful that the organisation would accept to be changed (this is costly!) and that the state would receive fewer income from taxes.

The ii examples suggest the following motto for significance testing: Never change a running organization. When comparing a new system with a well-tried organisation, always set the null hypothesis to the assumption that the new system is worse than the quondam ane. Then, if the null hypothesis is rejected, we can be quite certain that it's worth to replace the old system with the new one considering a type 1 error is unlikely.

How to select the significance level?

Typically the significance level is ready to 5%. If you are thinking about lowering the significance level, you lot should make certain that the examination you lot are nearly to perform has sufficient statistical ability. Peculiarly for minor sample sizes, lowering the significance level can critically increase the type two fault.

Assume we desire to utilise a t-test on the null hypothesis that drug B has less or equal mean effectivity than drug A. Then nosotros tin can utilize the power.t.test function from the pwr package. Assume that drug B exhibits a mean increment in effectivity larger than 0.5 (delta parameter) and that the standard difference of the measurements is one. Since we really want to avert type 1 errors here, we require a depression significance level of 1% (sig.level parameter). Let'south see how power changes with the sample size:

                library(pwr) sample.size <- c(10,20,30, xl, 50, 75, 100, 125, 150, 175, 200) power <- rep(NA, length(sample.size)) for (i in seq_along(sample.size)) {     n <- sample.size[i]     t <- power.t.test(northward = n, delta = 0.5, sd = one,                        sig.level = 0.01, alternative = "one.sided")     power[i] <- t$power } power.df <- information.frame("Due north" = sample.size, "Power" = power) library(ggplot2) ggplot(power.df, aes(x = N, y = Power)) + geom_point() + geom_line()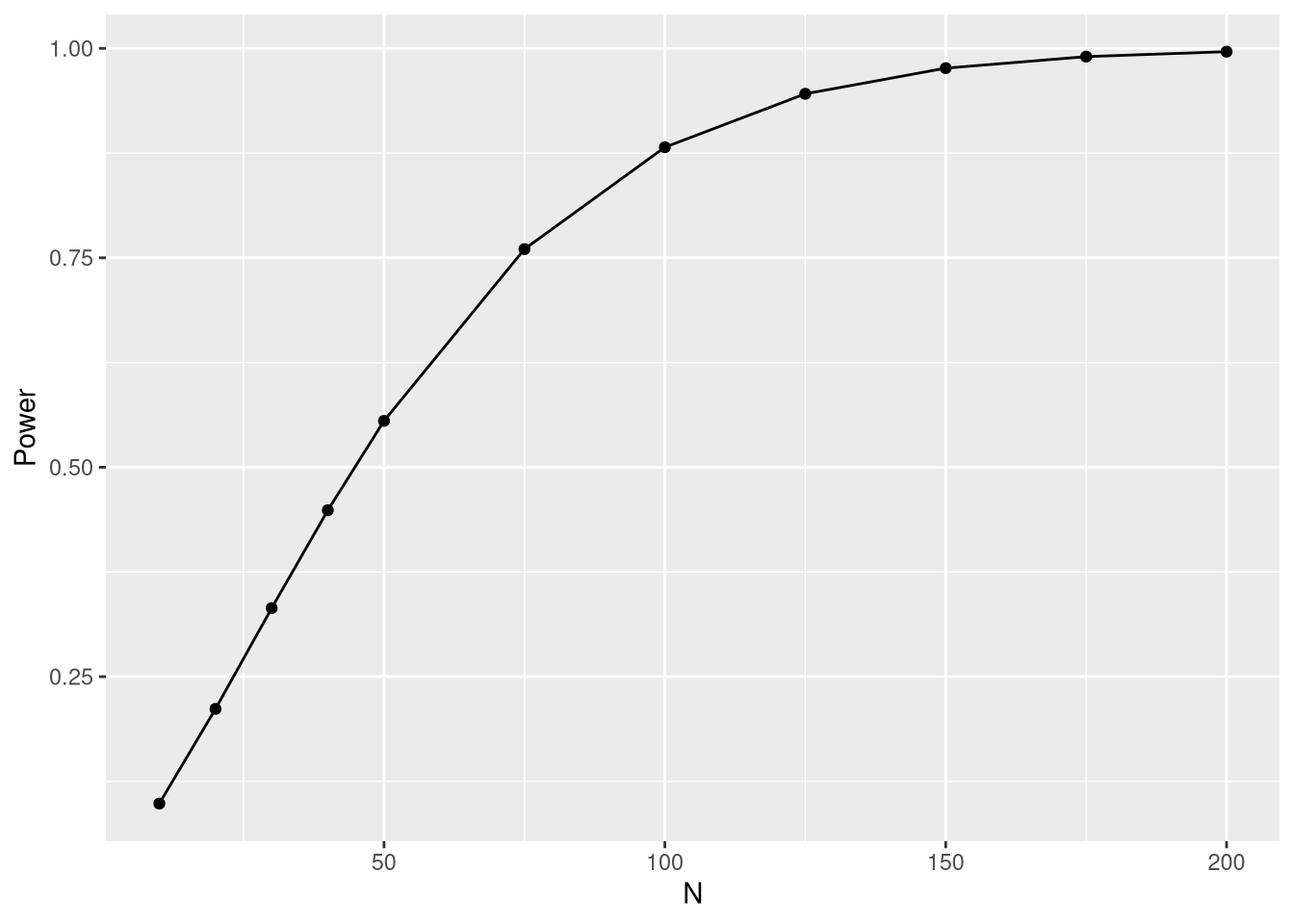

What do the results mean? For merely fifty measurements per group and a ane% significance level, the power would just be 55.5%. Then, if B were actually better than A, nosotros would fail to decline the zero hypothesis in 44.5% of cases. This type two error charge per unit is mode too high and thus a significance level of 1% should not be selected. On the other manus, with 150 samples per group we wouldn't have whatsoever issues because nosotros would have a type 2 error rate of 2.4% at the 1% significance level.

So, what should we exercise if the sample size is just fifty per group? In this example, nosotros would exist inclined to use a less stringent significance level. How lenient should it be? Nosotros tin can find out past requiring a power of 80%:

                t <- ability.t.exam(n = 50, delta = 0.5, sd = 1, ability = 0.8,                    sig.level = Cipher, alternative = "ane.sided") print(t$sig.level)              
                ## [i] 0.05038546

Thus, for 50 samples per grouping, acceptable ability would be obtained if the significance level is prepare to 5%.